- Get link
- X
- Other Apps
Note
This is my undergraduate assignment that I translated to English in the Electric Field Theory course where my task is to write an essay on the Amperes Law and Magnetic Fields. Apart from me this group consists of Vencisisca Jeane R, Rr. Sanita Eling Cipta Nesa, Putu Arie Pratama, Fajar Purnama, Muhammad Audy Bazly, Muhammad Nordiansyah. This assignment has never been published anywhere and we as the authors and the copyright holders license this task customized CC-BY-SA where anyone can share, copy, republish and sell on condition to state our name as the author and inform that the original and open version available here.
Chapter 1 Introduction
1.1 Background
In everyday life, many applications of several physical laws occur, one of which is Ampere's law and magnetic fields. Where in general the relationship between Ampere's law and magnetic fields, namely the Ampere's law states that the magnetic field can be generated in two ways, namely through an electric current (the initial formulation of the Ampere law), and by changing the electric field (Maxwell's addition). Maxwell's correction of the Ampere law is quite important, thus this law states that changes in the electric field can give rise to a magnetic field, and vice versa.
Three genius scientists from France, Andre Marie Ampere (1775-1863), Jean Baptista Biot (1774-1862) and Victor Savart (1803-1862) stated that the force will be generated by an electric current flowing in a conductor that is between the magnetic fields. This is also the reverse of Faraday's law, in which Faraday predicts that an induced voltage will arise in a moving conductor and cut across the magnetic field. This law is applied to electric machines, and the image below will explain this phenomenon.
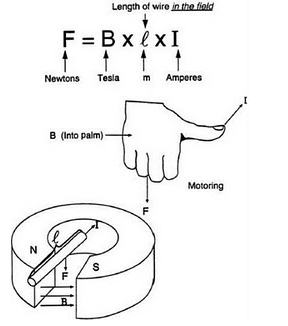
1.2 Problem
The problems raised in this assignment are as follows:
- What is the meaning of the Ampere's law and magnetic field?
- How is the relationship between current density and magnetic field?
- What is magnetic flux density?
- What is meant by magnetic vector potential and how is it applied?
- What is the stokes theorem?
1.3 Objective
The main purpose of writing the assignment "Ampere Law and Magnetic Field" this time is to know and understand in detail about Ampere's law and magnetic fields. The other objectives of this paper are:
- Able to define and explain Ampere's law and magnetic field.
- Find out how the relationship between current density and magnetic field.
- Able to define and know magnetic flux density.
- Able to explain the meaning of potential vectors and be able to explain how it is applied.
- Be able to define the stikes theorem.
1.4 Benefit
The benefits obtained from the paper "Ampere Law and Magnetic Field" are as follows:
- Provides in-depth knowledge of Ampere law and magnetic fields.
- Provides knowledge of the relationship between current or current density and magnetic fields.
- Gives knowledge about the vector potential that can be determined from the flow.
1.5 Scope of Material
In this assignment, the scope discussed by the author is limited to the issues discussed, namely the Ampere Law and Magnetic Fields.
Chapter 2 Discussion
2.1 Biot-Savart Law
The magnetic field differential, dH is the result of the current element differential I dH. The field is inversely proportional to the distance (r2), is a free medium that is around it and has a direction which is the cross product of I dI and aR. This relationship is known as the Biot-Savart Law, where the equation can be, seen as below:
dH = (I dI x aR)/(4πR2) (A/m)
The direction of R must come from the current element at the point where dH has been determined, as in the following figure:
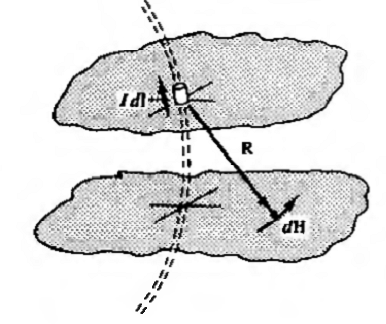
Current elements must not be separated. All elements complement the current filament contribution to H and the current must be involved. The integral form in Biot-Savart's Law is as follows:
H = ∮(I dI x aR)/(4πR2)
A simple closed integral requires all the current elements involved in obtaining the H.
Example Problem 1:
Current I is long and straight along the z-axis of the cylindrical coordinates as shown in the figure below.
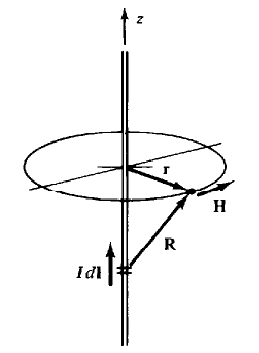
Without losing any of its general properties, choose a point in the z = 0 plane. Then in its differential form, it is as follows:
dH = (I dz ax X (rar X zaz) / (4π(r2+z2)<sup>(3⁄2))
= (I dz ra∅) / (4π(r2+z2)(3⁄2))
H = [∫-∞∞(Ir dz) / (4π(r2+z2)(3⁄2))] a∅
= a∅/2πr
The magnetic field by surface currents and volume is also given by the Biot-Savart law of integral form, where I dI is replaced by K dS or Jdv respectively, and where the integral is taken over the entire surface, or volume, concerned. An important example is the current in an infinite plane with a constant density K. Where the equation can be seen as follows:
H = K/2 X an
2.2 Ampere Law
The line integral of the tangential component H along the closed path is equal to the magnitude of the current in the vicinity:
∮H.dI = Ienc
This is Ampere's law. At first sight, we might think that the application of this law is to determine flow by an integration. In fact, usually the current is known and this law will give us a way of determining H. So the application of the law is very similar to using Gauss's law to determine D in a given charge distribution.
To be able to take advantage of Ampere's law in determining H there must be a sufficiently high degree of symmetry to the problem being discussed. The two conditions that must be met are as follows:
- H must be normal or tangential at each point of its path.
- H has the same or constant value for each point of its path, if H is tangential.
The Biot-Savart law can be used to determine which path meets these conditions. But in most cases, the path is immediately visible.
Example Problem 2:
Use the amperes law to get H by a long, straight current I. The Biot-Savart law shows that H is tangential and with the same magnitude along the circle in Figure 2.3, then the equation is as follows:
∮H.dI=H(2πr)=I
H = aϕ/2πr
2.3 Curl
The curl of the vector field A is another vector field. Point P in Figure 2.3 is located in the area ∆S which is bounded by closed curve C.
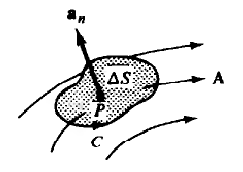
In the integration that defines curl, C is the area traversed by the curl so that the closed area is on the left. Normal units, determined using the rule of thumb, are as shown in the figure. Thus, the curl component of A in the direction an is defined as follows:
(curl A).an = lim(∆S→0)(∮A.dI/∆S)
In the coordinate system, curl A is the fully specified value defined by the component along the three vector units. For example, the x component of Cartesian coordinates is defined by taking the contour line C of the square in the plane x = conts, via the point P, as shown in Figure 2.5:
(curl A).an = lim(∆y ∆z→0) (∮A.dI / ∆y ∆z)
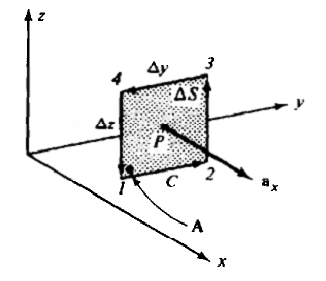
If, A = Axax + Ayay + Azaz, at the angle from closed ∆S to the center (point 1), then:
∮ = ∫12 + ∫23 + ∫34 + ∫41
=Ay∆y + (Az+(∂Az/∂y∆y))∆z + (Ay+(∂Ay/∂z∆z))(-∆y) + Az(-∆z)
=((∂Az/∂y)-(∂Ay/∂z)) ∆y∆z
(curl A).ax = (∂Az/∂y)-(∂Az/∂z)
The y and z components can be determined in the same way. The combination of the three components can be seen in the equation below:
curl A = ((∂Az/∂y)-(∂Az/∂z)) ax+((∂Ax)/∂z-(∂Az)/∂x) ay+((∂Ay)/∂x-(∂Ax)/∂x) az (cartesian)
The third-order determinant can be written like the equation below, the expansion of which gives the Cartesian curl of A.
curl A=|(ax&ay&az @ ∂/∂x&∂/∂y&∂/∂z @ Ax&Ay&Az)|
The elements of the second line are components of the del operation. This shows that ∇ × A can be written for curl A. As with other expressions of a vector analysis, this notation is used for curl A in other coordinate systems, even though × A is defined in Cartesian coordinates only.
The expressions for curl A at the coordinates of the cylinder and the sphere can be derived in the same way as above. Although, with a higher difficulty.
curl A = (1/r (∂Az)/(∂∅) - (∂A∅/∂z)) ar + ((∂Ar/∂z) - (∂Az/∂r)) a∅ + ((∂(rA∅))/∂r - (∂Ar/∂∅)) az (cylinder)
curl A = 1/(r sin ) [(∂(A∅ sinθ))/∂θ - (∂θ/∂∅)] ar+1/r [1/sinθ (∂Ar/∂∅)-(∂(rA∅)/∂r)] a∅ + 1/r [(∂(rA∅))/∂r-(∂Ar)/(∂∅)] az (spherical)
The frequency of use of the two properties of the curl operator can be explained as follows:
- The difference from curl is scalar zero, that is: ∇. (∇ × A) = 0 for each vector field A
- The curl of the gradient is zero vector, that is: ∇. (∇f) = 0 for any scalar function of position f (see problem) Under static conditions, E = -∇V, so ∇ × E = 0
2.4 The relationship of J and H
In the law of amperes, the equation definition of (curl H) x can be written as follows:
(curl H).ax=lim(∆y ∆z→0)Ix/(∆y ∆z)- Jx
Where Jx = dlx⁄dS is the area of density in x direction of current. So that the x component of curl H and direction of current J are the same at every point. Likewise for the x and y components, it can be seen as follows.
∇×H=J
This is one of Maxwell's equations in the static electric field. if H is known for the entire region, then ∇ × H = J will produce J for the region.
Sample Problem 3:
A conductor whose cross-section length is straight with radius a has a magnetic field strength H = (Ir⁄2πa2) in the conductor (r
J = ∇×H = -∂/∂z (Ir/(2πa2 )) ar+1/r ∂/∂r ((Ir2)/(2πa2 )) az = I/(πa2)az
which corresponds to the current of magnitude I in the + z direction which is evenly distributed over the cross-sectional area of πa2. Outside the conductor,
J = ∇×H = -∂/∂z (I/2πr) ar+1/r ∂/∂r (I/2π) az = 0
2.5 Magnetic Flux Density B
Like D, the magnetic field strength H depends only on the (moving) charges and does not depend on the medium. The force field with respect to H is the magnetic flux density B, given by:
B = μH
Where = μo μr, is the permeability of the medium and the unit of B is tesla.
1 T = 1 N/(A .m)
The permeability of the vacuum μ0 has a value of 4π × 10(-7) and the unit of henry per meter H⁄m, the relative permeability of μr medium is a pure number very close to unity.
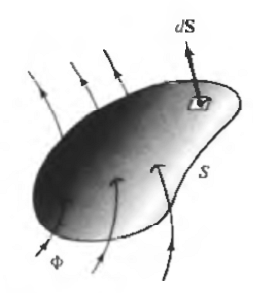
Magnetic flux Φ, which passes through a surface is defined as follows.
Φ = ∫SB .dS
The sign can be positive or negative depending on the choice of normal direction on dS and the unit of flux is weber, Wb. The different magnetic units are linked by the following equation.
1 T = 1 Wb⁄m2 1 H = 1 Wb⁄A
Example Problem 4:
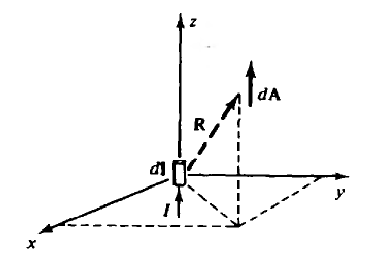
Determine the magnitude of the flux through the part of the plane ϕ = π⁄4 which is determined by 0.01 B = μ0 H = (μ0 I/2πr) aϕ dS = dr dz aϕ Φ = ∫02∫0,010,05(μ0I/2πr) aϕ dr dz aϕ =(2μ0I/2π) ln0,05/0,01 =1,61×10(-6) Wb =1,61 μWb It should be noted that the magnetic flux lines Φ are closed curves (curves), which have no starting and ending points. This differs from the electric flux ψ which originates from a positive charge and ends up being negatively charged. As shown in Figure 2.5, all flux lines Φ that enter a closed surface will come out again from that surface. Therefore, field B has neither a source nor a hole, which is mathematically expressed by the following equation. ∇.B=0 Initially, the electric field E is obtained from a known charge configuration. Later developed an understanding of the electric potential V, where E we see can be obtained as negative from the gradient, namely E = -∇V. Laplace's equation then provides a means of obtaining V from the knowledge of the potential magnitude at the conductive boundaries. Similarly, the magnetic vector potential A is defined such that, ∇ X A = B serves as an intermediate quantity, from which B and H. can be calculated. Note that the definition of A is consistent with the terms ∇. B = 0. The unit of A is Wь / m or Hm. If additional conditions are applied, then: ∇∙A=0 Then the potential vector A can be determined from the known currents in the area under study. For the three types of standard current configurations, the equations are as follows: Filament Current: A = ∮(μIdI/4πR) surface current: A = ∫S(μKdS/4πR) volume flow: A = ∫v(μJdv/4πR) Here R is the distance of the current element at the point where A is to be calculated. As with similar integrals for electric potential, the equations for A above are based on the assumption of a zero price level at infinity; therefore, the previous formulas cannot be used if the currents themselves continue to infinity. Sample Problem 5: Check the magnetic potential vector for a long straight line I of current, in free space. In Figure 2.7 the current is along the z-axis and the field points are (x, y, z). Also shown is a current element I dI=Idl az At l = 0, where l is the variable that changes along the z-axis. It is clear that integral, A = ∫(-∞)∞(μ0 I dl/4πR) az However, it is possible to consider a differential potential vector. dA = (μ0 I dl/4πR) az And obtain from it the differential B. Thus, by the special current element at l = 0, we have dA=(μ0 I dl)/(4π(x2+y2+z2)(1⁄2) ) ax dB=∇×dA =(μ0 I dl/4π) [(-y)/(x2+y2+z2)(3⁄2) ax+x/(x2+y2+z2)(3⁄2) ay ] This result corresponds to the dH = (I⁄μ0)dB given by the Biot-Savart law On an open surface S bounded by a closed curve C. Stokes' theorem says that the tangential component integral of the vector field F along C is the same as the normal component integral of the curl F through the surface S: ∮F.dl = ∫s(∇×F).dS If F is chosen to be the magnetic potential vector A, then Stokes' Theorem can be formulated as follows: ∮A.dl = ∫sB.dS = Φ The conclusions that can be drawn from this paper are as follows: After the authors made this assignment, the suggestions that can be suggested are in performing calculations using the above formulas, one should properly master the concepts in their use, so that there are no fundamental errors in the process.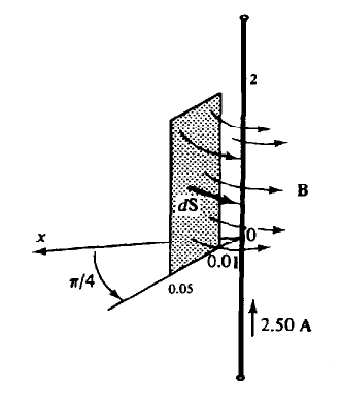
2.6 Magnetic Vector Potential A
2.7 Stokes' theorem
Chapter 3 Closing
3.1 Conclusion
3.2 Suggestion
Bibliography
Mirror
- Get link
- X
- Other Apps
Comments
Post a Comment